How technological choices, existing portfolios, and multi-dimensional price risk affect power generation investments
by Wilko Rohlfs and Reinhard Madlener (IAEE Energy Forum Newsletter Second Quater 2016 p. 7-9)
Fossil-fueled power plants with high efficiencies are typically large-scale and long-lived projects (40-60 years of lifetime plus substantial construction/lead times). These attributes incur high upfront – and more or less irreversible – investments, which result in risky and long-term business undertakings. Price projections and estimates of the technological progress of new and existing technologies need to be considered in the decision-making process. And although continuous plant maintenance and retrofitting enables the preservation (or, due to technical innovation, even a slight increase) of the conversion efficiency over a plant’s lifetime, the main process remains unaltered. Hence, the pre-investment decision with regard to the input fuel to be used for conversion into electricity is crucial for the entire lifetime of such a power plant.
Power generation technologies vary in their technical, economic, and environmental characteristics. Cash flows generated from the operating of a power plant are a result of a technology-specific mix of inputs and outputs, and they are dependent on expenditures for fuel, carbon emission permits, and revenues from electricity sales, all of which are themselves dependent on their respective price. As a consequence, different types of power plants (in our research, gas- or coal-fired, with or without carbon dioxide sequestration, as well as onshore and offshore wind) exhibit different capital expenditures and differ with regard to the specific combination of the underlying commodities. This combination can be viewed as a portfolio of real assets. Importantly, the prices of the underlying commodities are correlated with each other, and the price development in deregulated markets is usually highly uncertain.
Decision-making under multi-dimensional price uncertainty
Decision-making with respect to long-lived irreversible energy investments under uncertainty calls for multi-dimensional models that are able to account for the unknown price trajectories of all the different prices of the underlying commodities (fuel input, CO2 permits, and electricity output). Figure 1 depicts some possible future development paths of the electricity price (upper plot) and the correlation between the coal and electricity prices for possible future states (lower plot). In the analysis, trend and volatility values for the commodity prices are derived from the price trajectories for Germany reported in Nitsch et al. (2010).
For such scenario analysis, deterministic approaches are commonly used that assume a constant rate of change for each price and vary it within an expected or realistic range (Ventosa et al., 2005). More sophisticated approaches for dealing with price uncertainty make use of stochastic models, which can be classified according to Möst & Keles (2009) into those that
- use stochastic processes for electricity prices, commodity prices, and other uncertain parameters (such as hydro inflows, solar irradiation, or wind distributions);
- enable scenario generation and reduction;
- allow the stochastic optimization of investment decisions, including short- and mid-term electricity generation planning and long-term system optimization.
Commonly employed stochastic net present value (NPV) approaches enable a comparison of the expected value of the different technologies in each state, from which the technology with the highest expected rate of return can subsequently be chosen. Although this decision process can be seen as a kind of optimization, it is nevertheless a static approach that does not account for (net) economic gains accruing from a delaying of the investment decision (and investing only if prices are developing in a favorable direction). In contrast, real options-based (RO) models (originally developed by Black and Scholes (1973) and Merton (1977) for financial options) can include this value of waiting (McDonald and Siegel, 1986), thus optimizing the decision process also over time (Dixit & Pindyck, 1994). In recent years, the application of RO models to decision-making processes in the energy sector, especially for investments in new power generation infrastructures, has increased considerably (for a literature review, see, e.g., Martínez Ceseña et al., 2013).
In a recent study by the authors, a generalized RO model has been developed that, in contrast to more conventional RO models used, accounts for multiple commodities by correlated stochastic price paths with a combined evaluation of an arbitrary number of available technologies.
How to discount future cash flows of multi-dimensional investment options
The discount rate is one of the most important parameters – possibly the most important one – in economic analysis of investments with a long lifetime. It can drastically affect the expected value of an investment, and it thus renders the comparison of results from different studies almost impossible if the internal rate of return is not calculated.
A more sophisticated choice of the discount rate than a practitioner’s rule of thumb accounts for the technology-specific project risk profile that itself results from the technology-specific combination of the underlying commodities, provided that these show different but correlated price uncertainties. Thus, a combination of commodities (i.e. cash flows generated from expenditures and returns) leads to a portfolio of commodities (or assets) in which the uncertainty can vanish if the risks of the assets are uncorrelated, similarly to the standard mean-variance portfolio theory of Markowitz (1952, 1991). Consequently, risk becomes endogenous, as a technology-dependent measure used for risk-adequate discounting – in the sense of the classical capital asset pricing (CAPM) model of Sharpe (1964) and Lintner (1965) – and requires a technology-dependent discount rate. However, this endogenous discounting faces two main complications, namely time-dependent risk structures and inter-temporal correlations of asset prices. Both aspects will be outlined in the next two paragraphs.
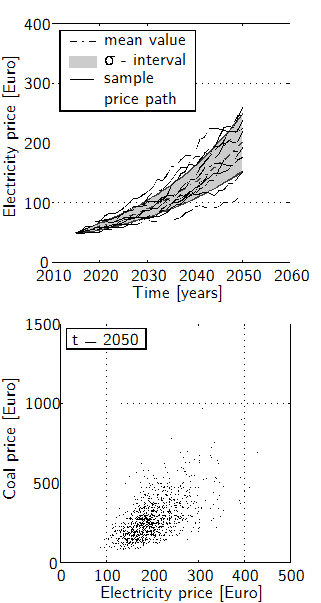
Sample paths of the price development (upper plot) and correlation between two assets (coal and gas) in t = 2050 (lower plot), both calculated by a Monte Carlo simulation technique (Source: Rohlfs & Madlener, 2014a).
First, assuming constant values of key parameters (e.g. growth rate and volatility) for the stochastic processes of the underlyings (i.e. asset prices), the risk of the prospective returns becomes time-dependent if the ratios between input and output quantities are fixed. For the desired dynamic optimization of the investment strategy, the RO approach is well suited, as it incorporates the value of waiting. Nevertheless, multi-asset option models typically assume that, once the investment has been made, the share of the different underlyings will remain constant over time, which leads to a time-invariant solution. However, in the case of power plants, the technology chosen defines the input and output quantities as well as the ratio between them for the entire lifetime of a plant. Such a constant ratio between the input and output quantities couples the prospective returns directly to the ratio between the asset prices. The unequal growth rates predicted for the prospective prices cause a strong time-dependency in the ratio between the various input and output cash flows, and thus also cause time-varying levels of uncertainty.
Second, the evaluation of uncertain cash flows gained at different times is more complex in comparison to the evaluation of stocks in a financial portfolio. Due to strong correlations of subsequent returns, a separate valuation of the resulting cash flows remains inaccurate. The following example illustrates the problem. Let us suppose that an uncertain cash flow in period 1 takes the value of either 100 or 200 (for simplicity, with the same probability). Due to uncertainty, a risk premium would be required, reducing the expected utility to below the utility of the average cash flow of 150. In period 2, the same cash flow might be gained, but due to a temporal correlation, the cash flow is 100 if the cash flow of the previous period was 200, and vice versa. A segregated treatment of the two periods would again require a risk premium. However, by evaluating the cash flows jointly, the associated risk vanishes if the time between the two cash flows is sufficiently short. This simple exercise illustrates how intertemporal correlations between different cash flows preclude the use of simplistic discounting methods when combining risk-discounting with time-discounting.
How existing power plant portfolios influence the optimal investment decision
In a recent study, we have developed and applied a multi-dimensional model with time-, technology- and state-dependent discount methodology (Rohlfs and Madlener, 2014a, 2014b). The proposed generalized model also enables, for example, an examination of the influence of new investments on existing power plant portfolios, as is shown by Rohlfs and Madlener (2014a) and illustrated in Fig. 2. The figure depicts an estimated probability for the deployment of different generation technologies. The probability is based on technological specifications and price projections up to 2070. Price projections for electricity, coal, natural gas, and carbon permits were calculated based on the predictions of the so-called German Pilot Study 2010 (Nitsch et al., 2010). The technologies considered comprise hard coal (HC), hard coal integrated gasification combined cycle without (HC-IGCC) and with carbon capture and storage (HC-IGCC-CCS), combined gas and steam power plant without (COGAS) and with CCS (COGAS-CCS) as well as onshore wind (OW). In the remainder of this article, we summarize the findings of the above mentioned study (Rohlfs and Madlener, 2014a, p.125).
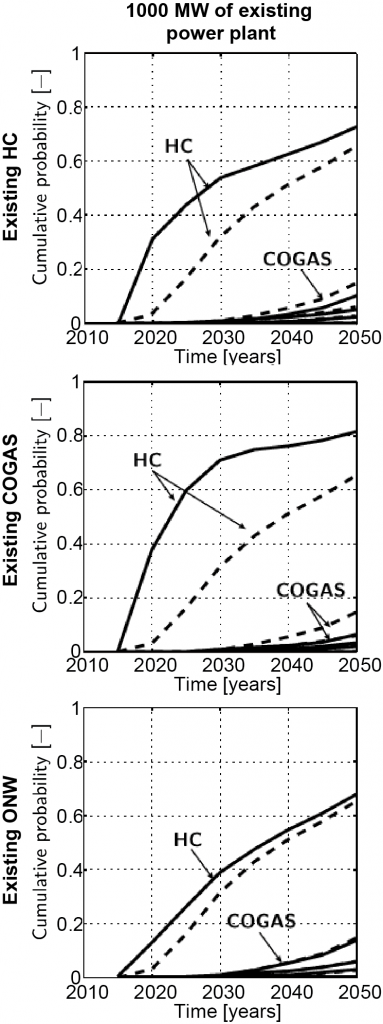
Influence of existing power plants on the investment decision when taking the value of waiting into account. The dashed lines indicate the investment decision for the case of no preexisting portfolio. (Source: Rohlfs & Madlener, 2014a).
In a first step, we have employed the classical NPV model as well as the RO approach to identify the influence of the different aspects of the RO model (e.g. value of waiting, multiple available technologies, and existing power plant portfolios). For an investment in a new power plant today, the NPV is highly negative, rendering an investment economically very unattractive. When tracking the decision into the future, a significant increase in the probability of investing in coal-fired power plants was found (beyond 2020), and for later time periods also the probability of coal-fired power plants equipped with CCS increases. However, if an investor has the choice of building one of the power plant technologies available, then the dominance of one technology strongly reduces the probability of investments in other technologies.
With the value of waiting in the decision process, the expected value (RO value) increases above the expected NPV, although the investment decision is delayed. It is interesting to note that the value of waiting also reshapes the probability distribution of the expected values and, consequently, the associated risk. While for the classical NPV decision rule, the probability distribution of future NPVs is more or less Gaussian-shaped, the probability of the value of waiting is strongly asymmetric. The asymmetric shape reveals a steep gradient (decreasing probability) for expected values below zero and a long tail for positive expected values. Consequently, the probability of falling below the desired rate of return, i.e. a negative expected value, yields a strong reduction if the value of waiting is considered.
Accounting for an existing power plant portfolio of an investor changes the decision if the value of waiting is considered. Because systematic risk between new and existing projects can be dispunged, the resulting volatility diminishes, leading to a reduced value of waiting and thus to a preponed investment. Owing to the hard coal power plant’s dominance, this effect has the most significant impact on investors who already have gas-fired power plants in their fleet of generation units.
A further advantage of using the proposed RO model was revealed in a sensitivity analysis, which showed that the decision process is less influenced by the choice of the discount rate if the value of waiting is considered, compared to the classical NPV decision rule. Thus, the value of waiting enables a more robust estimation of the probability of future investments.
Economic decision-making models for long-lived investments are very sensitive to the assumptions made with regard to the prospective price development and, as such, can never accurately predict the future. Evidence is provided by the struggling electric utility companies in Germany that are suffering from the high share of intermittent renewables and the rapid nuclear phase-out. However, economic modeling itself provides useful insights, broadening a decision-maker’s horizon and sharpening an investor’s sensitivity to crucial parameters and effects. By tackling questions related to the “correct” way of discounting and the influence of portfolios in the decision process, the RO models developed in recent years enable such powerful and potentially useful insights.
References
Black, F., Scholes, M., 1973. The pricing of options and corporate liabilities. Journal of Political Economy 81 (3), 637–654.
Dixit, A. K., Pindyck, R. S., 1994. Investment under Uncertainty. Princeton University Press, Princeton, N.J.
Lintner, J., 1965. The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. The Review of Economics and Statistics 47 (1), 13–37.
Markowitz, H. M., 1952. Portfolio selection. Journal of Finance 7, 77–91.
Markowitz, H. M., 1991. Foundations of portfolio theory. The Journal of Finance 46 (2), 469–477.
Martínez Ceseña, E.A., Mutale, J., Rivas-Dávalos, F., 2013. Real options theory applied to electricity generation projects: A review, Renewable and Sustainable Energy Reviews 19 (March), 573-581.
McDonald, R., Siegel, D., 1986. The value of waiting to invest. The Quarterly Journal of Economics 101 (4), 707–727.
Merton, R., 1973. The theory of rational option pricing. Journal of Economic Management Science 4 (1), 141–183.
Möst, D., Keles, D., 2009. A survey of stochastic modelling approaches for liberalized electricity markets. European Journal of Operational Research 207 (2), 543–556.
Nitsch, J., Pregger, T., Scholz, Y., Naegler, T., Sterner, M., Gerhardt, N., von Oehsen, A., Carsten, P., Saint-Drenan, Y.-M.,Wenzel, B., 2010. Langfristszenarien und Strategien für den Ausbau der erneuerbaren Energien in Deutschland bei Berücksichtigung der Entwicklung in Europa und global – Leitstudie 2010. Bundesumweltministerium BMU – FKZ 03MAP146.
Rohlfs, W., Madlener, R., 2013b. Investment decisions under uncertainty: CCS competing with green energy technologies. Energy Procedia 37, 7029–7038.
Rohlfs, W., Madlener, R., 2014a. Optimal Power Generation Investment: Impact of Technology Choices and Existing Portfolios for Deploying Low-Carbon Coal Technologies, International Journal of Greenhouse Gas and Control 28, 114-125.
Rohlfs, W., Madlener, R., 2014b. Multi-Commodity Real Options Analysis of Power Plant Investments: Discounting Endogenous Risk Structures. Energy Systems J., 5 (3), 423-447.
Sharpe, W., 1964. Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance 19 (3), 425–442.
Ventosa, M., Baillo, A., Ramos, A., Rivier, M., 2005. Electricity market modeling trends. Energy Policy 33, 897–913.